What are Bearings in Maths?
A bearing is a measurement of the movement of an angle in a clockwise direction and always on the north line.
The bearing of a point is the line joining the centre of the compass through the point measured in degrees in a clockwise direction from the north heading. Bearings are used to indicate direction as well as the angle of a particular landmark.
Bearings in Maths GCSE are three digit angles measured clockwise from the 0° point of a protractor.
The north direction (or starting point) is usually provided in the question text on your GCSE maths exam. You then need to measure the required angle in a clockwise direction.
All bearings in Maths must be given in three digits, so if the measured angle is less than 100°, you must start the three-digit bearing with a zero, so the 30° clockwise angle increase from the north (or 0°) is usually written as 030°.
Bearings can be the angle between two objects, or bearings from an object to a point on the ground.
There are a few things to keep in mind when using bearings in Maths:
– Bearings are always measured clockwise from the north or 0° point on a protractor/angle measurer.
– Bearings should be given as three-figures (such as 030°).
Measuring bearings in a GCSE Maths exam
When you are given a bearing based question in your GCSE maths exam, you will be required to measure the angle using a protractor.
For example, if you are given a bearing of 030°, this means that you should measure an angle of 30° clockwise from the north (as defined on the examination paper).
When you are measuring bearings, it is important to be precise so that you get the correct answer in your exam.
How to draw bearings in Maths
- Locate the point where you’ll be measuring the bearing and draw a north line if one isn’t already there.
- Place the zero of the protractor on the north line and measure the required angle clockwise, creating a mark on your page at that angle.
- Draw a line from the start point in the direction of the bearing (around the outside edge of the protractor). If you’re creating a scale drawing and know how far away to place a point, use this scale.
Use of sine and cosine rules
The sine and cosine rules can be used to calculate bearings in your GCSE maths exam.
These rules are based on the fact that the sine of an angle is equal to the length of the opposite side divided by the length of the hypotenuse.
The cosine of an angle is equal to the length of the adjacent side divided by the length of the hypotenuse.
Use the sine rule when:
- You need to find the length of one side and you know at least one other sides length and have three angles
- You need to find an angle and you know the length of two sides and one angle
Use the Cosine rule when:
- You need to find the length of one side and you have the length of two sides and the included angle
- You need to find an angle and you know the length of all three sides
Example Questions:
Question 1:
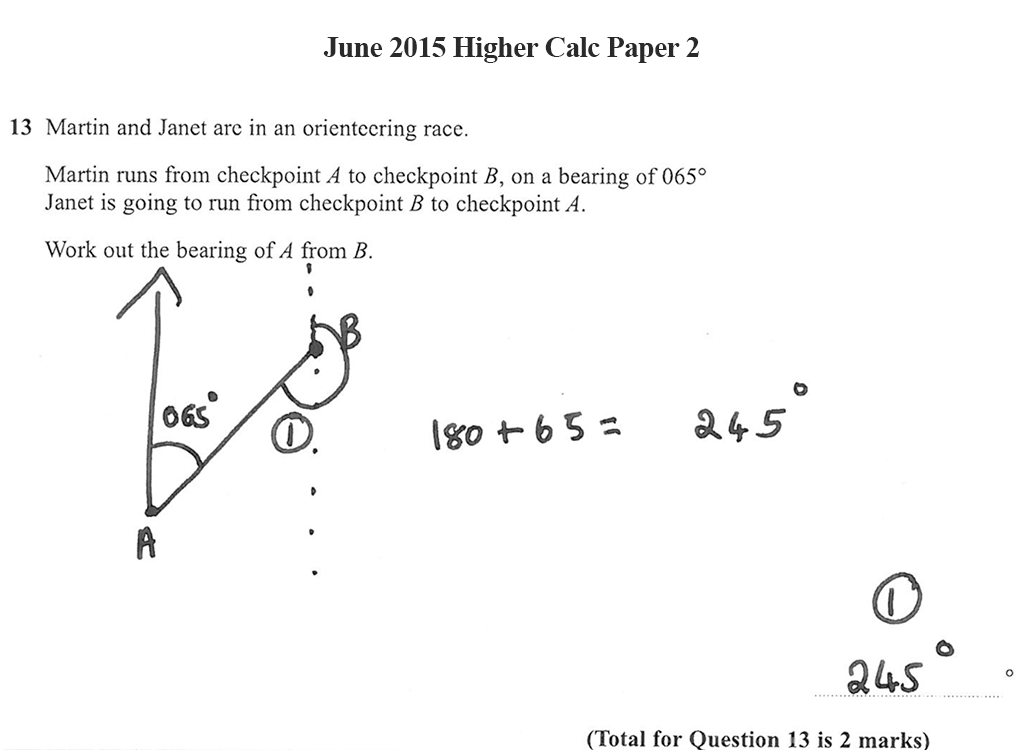
Martin and Janet are in an orienteering race.
Martin runs from checkpoint A to checkpoint B, on a bearing of 065°.
Janet is going to run from checkpoint B to checkpoint A.
Work out the bearing of A from B.
Explanation 1:
Question 2:
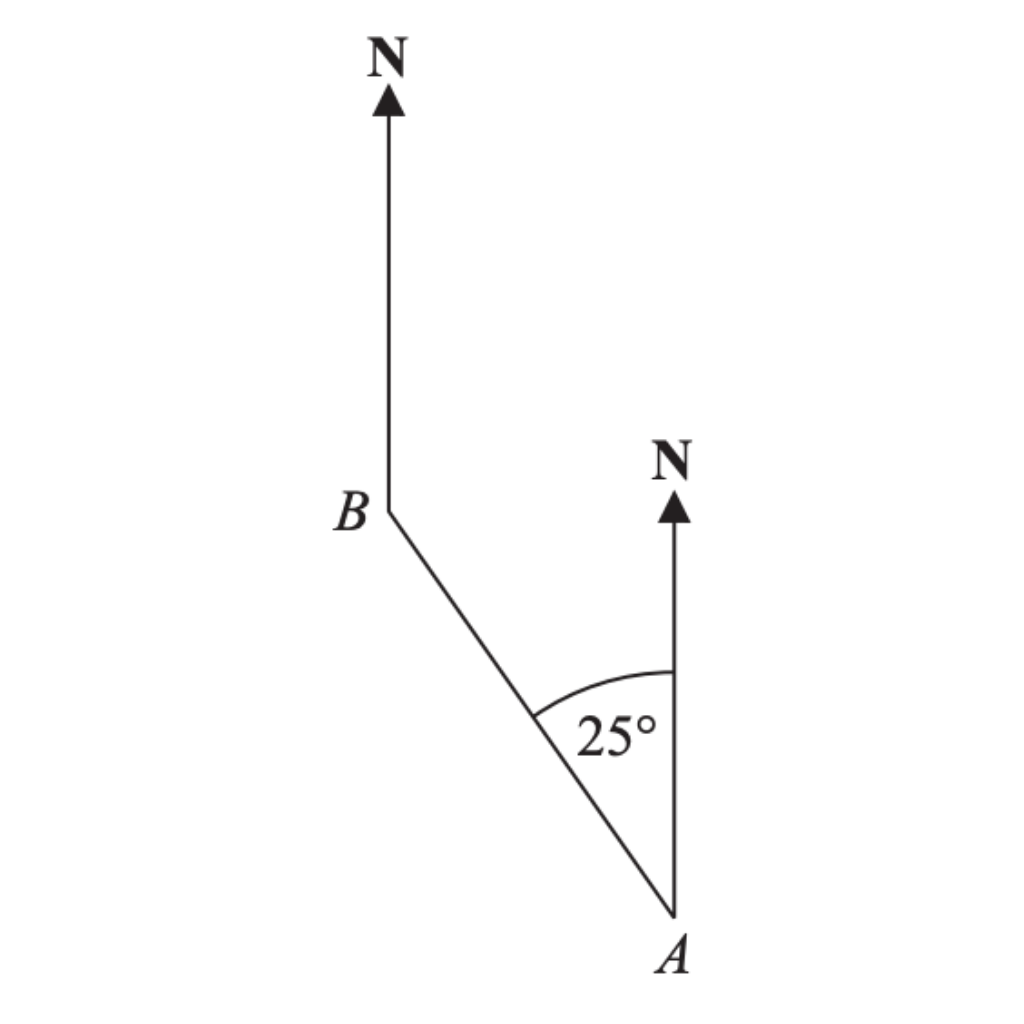
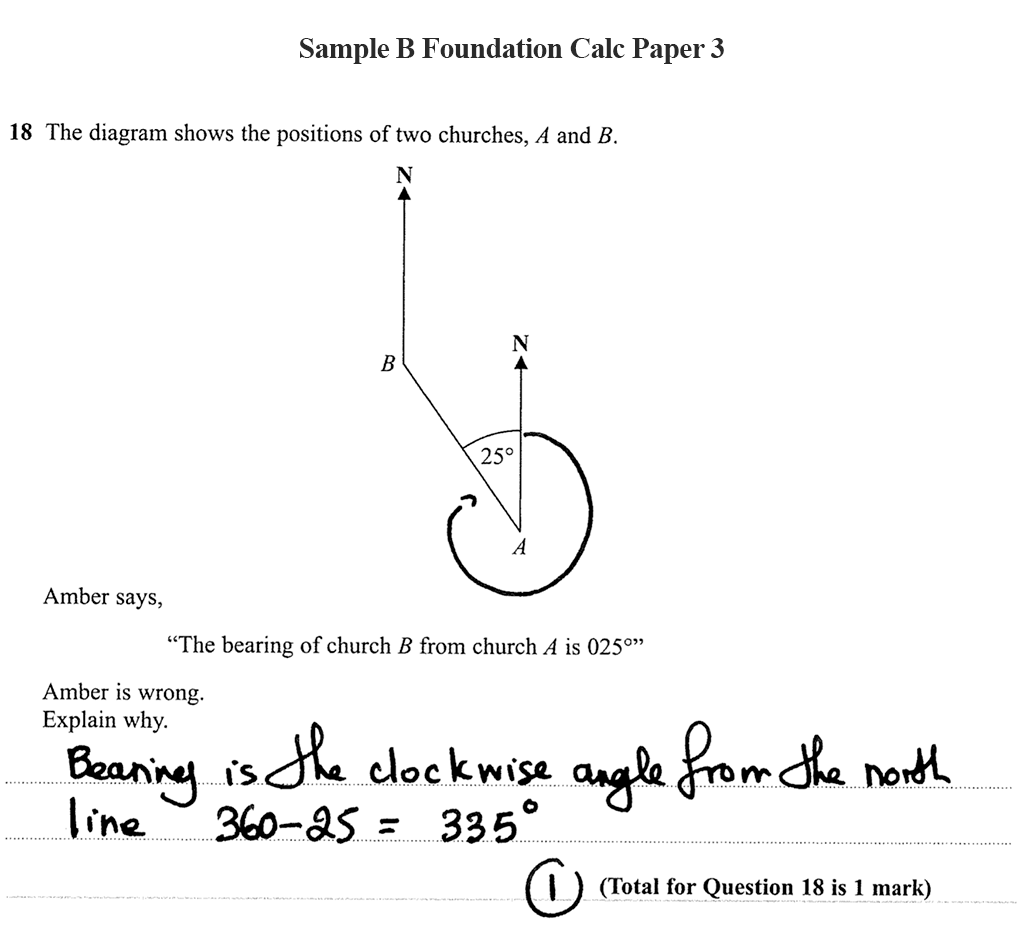
Amber says: “The bearing of church B from church A is 025°”
Amber is wrong.
Explain why.
Explanation 2:
Examples of bearings in everyday life
Bearings are a vital tool for navigation, whether you’re on land or at sea. They are not just used in GCSE maths, but also used in everyday life in a variety of ways.
For example, you can use them to indicate direction on maps and globes, or steer a ship and a boat along an axis of travel at sea. Bearings are also used in mathematical calculations. If you know that a certain landmark is at 270° bearing from where you’re standing, you can walk in that direction and eventually reach the landmark.
Now that you know the basics of bearings, you can put this knowledge to use in your everyday life!
Conclusion
Bearings are a relatively simple concept and can be very useful in a variety of situations.
You can use them in navigation on land and sea, as they can give you a quick and easy way to work out which route you need to take. You can also use bearings to specify directions on maps and globes. However, in most cases, you will need to know about bearings for your GCSE Maths exam.
When you’re studying for your exams, make sure to sign up to SchoolOnline to learn and practise more questions about bearings from our expert examiners.
Mini Glossary:
Three-Figure Bearings – The angle in degrees measured clockwise from North.
Hypotenuse – The longest side of a right-angled triangle, opposite the right angle.
Compass bearings – The 4 main directions of North, South, East, and West and in-between those bearings such as North-East etc.
How do you calculate Bearings in Maths?
To calculate bearing to degrees of a standard angle, you need to subtract the bearing angle from 90°. If your answer is negative, you need to add 360°. If the answer turns out to be more than 360° you need to subtract 360° from the answer.
What are the 3 rules of Bearings in Maths
1. Measure bearings from the North (given in the exam paper).
2. Give your answer in three-figure bearings (80° would be 080°).
3. Always draw and measure bearings clockwise.
What are bearings in Maths?
Bearings are angles that are measures clockwise from the north.


